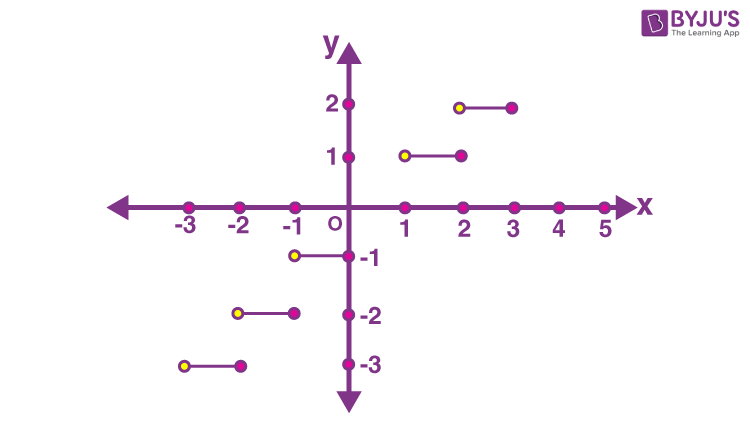
✅ Paloittain määritelty funktio koostuu eri osista, jokainen tietyllä alueella, tarjoten joustavuutta monimutkaisten ongelmien ratkaisuun.
Mitä tarkoittaa paloittain määritelty funktio matematiikassa
Paloittain määritelty funktio on matemaattinen käsite, jossa funktio määritellään eri lausekkeilla eri osille sen määrittelyaluetta. Tämä tarkoittaa, että funktio voi käyttäytyä eri tavoilla eri arvoilla, ja se voi olla erityisen hyödyllinen silloin, kun halutaan kuvata monimutkaisempia ilmiöitä, jotka eivät ole lineaarisia tai joiden käyttäytyminen vaihtelee tietyissä rajoissa.
Esimerkki paloittain määritellystä funktiosta
- f(x) = { 2x + 1, jos x < 0
- x^2, jos 0 ≤ x < 2
- 3, jos x ≥ 2
Tässä esimerkissä funktio f(x) ottaa eri arvoja riippuen siitä, mikä x:n arvo on. Esimerkiksi, jos x on -1, niin f(-1) = 2(-1) + 1 = -1. Jos x on 1, niin f(1) = 1^2 = 1, ja jos x on 3, niin f(3) = 3.
Miksi paloittain määritellyt funktiot ovat tärkeitä
Paloittain määritellyt funktiot ovat erityisen tärkeitä monilla aloilla, kuten insinööritieteissä, taloustieteessä ja tietojenkäsittelytieteessä. Ne mahdollistavat monimutkaisempien ilmiöiden mallintamisen ja analysoinnin, kuten esimerkiksi:
- Erilaiset taloudelliset mallit, joissa veroprosentti tai tuki voi muuttua eri tuloalueilla.
- Fyysiset prosessit, joissa materiaali käyttäytyy eri tavalla eri olosuhteissa.
- Ohjelmoinnissa, kun halutaan toteuttaa erilaisia toimintoja eri syötearvoille.
Paloittain määriteltyjen funktioiden käyttö
Kun käsitellään paloittain määriteltyjä funktioita, on tärkeää ymmärtää niiden jatkuvuus ja erotettavuus. Funktio voi olla jatkuva, mutta se ei välttämättä ole derivoituva rajoilla, joissa se vaihtaa määriteltyä lauseketta. Tämä voi vaikuttaa siihen, miten funktiota voidaan käyttää käytännön sovelluksissa.
Artikkelissani käsittelen paloittain määriteltyjen funktioiden ominaisuuksia, niiden graafista esittämistä ja soveltamista käytännön ongelmien ratkaisemisessa. Otan myös esille erilaisia esimerkkejä ja tilanteita, joissa paloittain määriteltyjä funktioita käytetään ja miten ne eroavat muista funktiotyypeistä.
Esimerkkejä paloittain määritellyistä funktioista ja niiden sovelluksista
Paloittain määritellyt funktiot ovat keskeisiä matematiikan ja insinööritieteiden alalla, ja niillä on monia käytännön sovelluksia. Tarkastellaanpa muutamia esimerkkejä, jotka havainnollistavat näiden funktioiden käyttöä eri tilanteissa.
1. Esimerkki: Regressiomalli
Paloittain määritelty funktio voi esiintyä esimerkiksi regressiomallissa, jossa datan mallit perustuvat tiettyihin kynnysarvoihin. Oletetaan, että meillä on myyntidataa, joka on jaettu kolmeen eri osaan:
- 0 – 100: Myynti on matala, ja tuote on vasta markkinoilla.
- 101 – 500: Myynti on keskimääräistä, ja tuote on saanut näkyvyyttä.
- yli 500: Myynti on korkea, ja tuote on markkinoiden ykkönen.
Tässä tapauksessa voimme määrittää paloittain määritellyn funktion myynnin perusteella. Esimerkiksi:
f(x) = {
0, jos x ≤ 100
1, jos 101 ≤ x ≤ 500
2, jos x > 500
}
2. Esimerkki: Raskausajan arviointi
Toinen esimerkki paloittain määritellystä funktiosta on raskauden arviointi. Raskauden kesto voidaan jakaa eri vaiheisiin:
- Ensimmäinen trimesteri: 0 – 12 viikkoa
- Toinen trimesteri: 13 – 26 viikkoa
- Kolmas trimesteri: 27 – 40 viikkoa
Voimme käyttää paloittain määriteltyä funktiota arvioidaksemme raskauden vaihetta:
f(x) = {
"Ensimmäinen trimesteri", jos 0 ≤ x ≤ 12
"Toinen trimesteri", jos 13 ≤ x ≤ 26
"Kolmas trimesteri", jos 27 ≤ x ≤ 40
}
3. Esimerkki: Liikennesäännöt eri nopeuksille
Paloittain määritellyt funktiot voivat myös auttaa ymmärtämään liikennesääntöjä ja -rajoituksia. Esimerkiksi nopeusrajoitukset voivat muuttua eri alueilla:
| Nopeusraja | Alue |
|---|---|
| 50 km/h | Kaupungin keskusta |
| 80 km/h | Taajama |
| 120 km/h | Moottoritie |
Tässä tapauksessa voimme määrittää paloittain määritellyn funktion liikennesääntöjen perusteella:
f(x) = {
50, jos alue = "Kaupungin keskusta"
80, jos alue = "Taajama"
120, jos alue = "Moottoritie"
}
Nämä esimerkit havainnollistavat, kuinka paloittain määritellyt funktiot voivat olla hyödyllisiä käytännön tilanteissa ja auttaa meitä ymmärtämään monimutkaisempia ilmiöitä. Ne tarjoavat myös selkeän tavan esittää ja analysoida dataa, erityisesti silloin kun muutokset tapahtuvat tietyissä kynnysarvoissa.
Usein kysytyillä kysymyksillä
Mitä on paloittain määritelty funktio?
Paloittain määritelty funktio on matemaattinen funktio, joka on määritelty eri säännöillä eri osille sen määrittelyjoukkoa. Tämä tarkoittaa, että funktio käyttäytyy eri tavoin eri väleillä.
Missä tilanteissa käytetään paloittain määriteltyjä funktioita?
Paloittain määriteltyjä funktioita käytetään usein matematiikassa, taloustieteissä ja insinööritieteissä, kun halutaan mallintaa ilmiöitä, jotka muuttuvat eri alueilla eri tavoin.
Voiko paloittain määritelty funktio olla jatkuva?
Kyllä, paloittain määritelty funktio voi olla jatkuva, jos se on jatkuva jokaisessa osassa ja osien rajat ovat yhteensopivia (eli eivät aiheuta hyppäyksiä).
Kuinka piirtää paloittain määritelty funktio?
Paloittain määritellyn funktion piirtämiseen tarvitaan jokaisen osan kaavan ymmärtäminen ja sen soveltaminen määritellyillä väleillä. Jokainen osa piirretään erikseen ja liitetään toisiinsa.
| Ominaisuus | Kuvaus |
|---|---|
| Määrittelyjoukko | Funktio määritellään eri säännöillä eri osille. |
| Jatkuvuus | Funktio voi olla jatkuva, jos osien rajat ovat sopusoinnussa. |
| Esimerkki | f(x) = { x^2, x < 0; x + 1, x ≥ 0 } |
| Pitoisuus | Paloittain määritellyt funktiot voivat olla helposti laskettavissa ja analysoitavissa. |
Toivomme, että tämä artikkeli auttoi sinua ymmärtämään paloittain määriteltyjä funktioita paremmin! Jätäthän kommenttisi ja tarkista myös muut artikkelit verkkosivustollamme, jotka saattavat kiinnostaa sinua.